The URDF file encodes all the information regarding dimensions, weight, inertias and meshes that are required for realistic simulation.


Steps	Screenshots
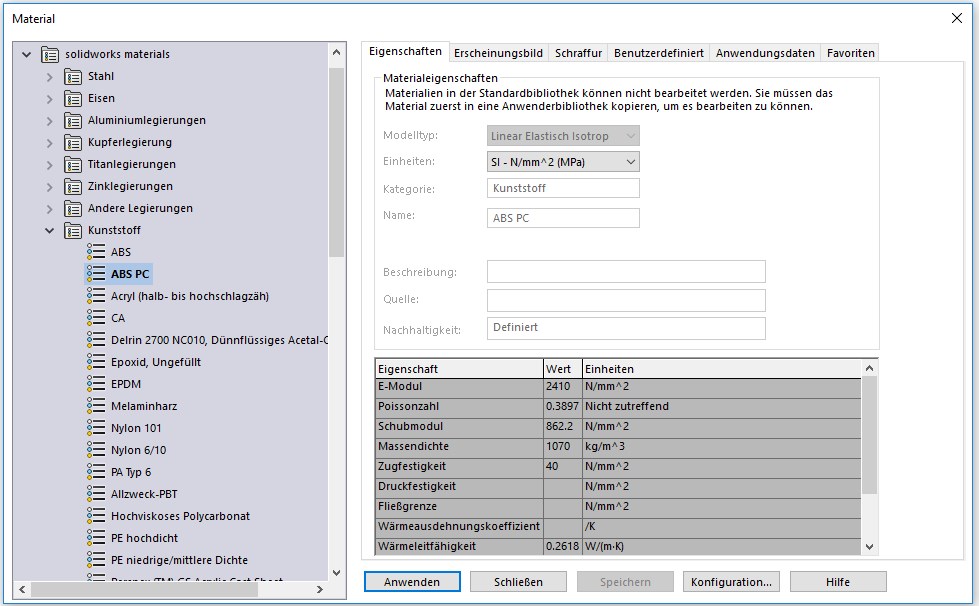
For calculating the inertias in Solidworks the mass properties have to be set correctly for all of the subcomponents. For parts with constant density set the material properties to the right material. For the 3d printed parts I use the following materials: Fortus PC or Duraform HST → Solidworks Material ABS PC with density of 1070 kg/m3 Projet MX3 Material → PMMA with density of 1190 kg/m3 Stainless Steel Screws → 1.4000 X6CR13 with density of 7700 kg/m3
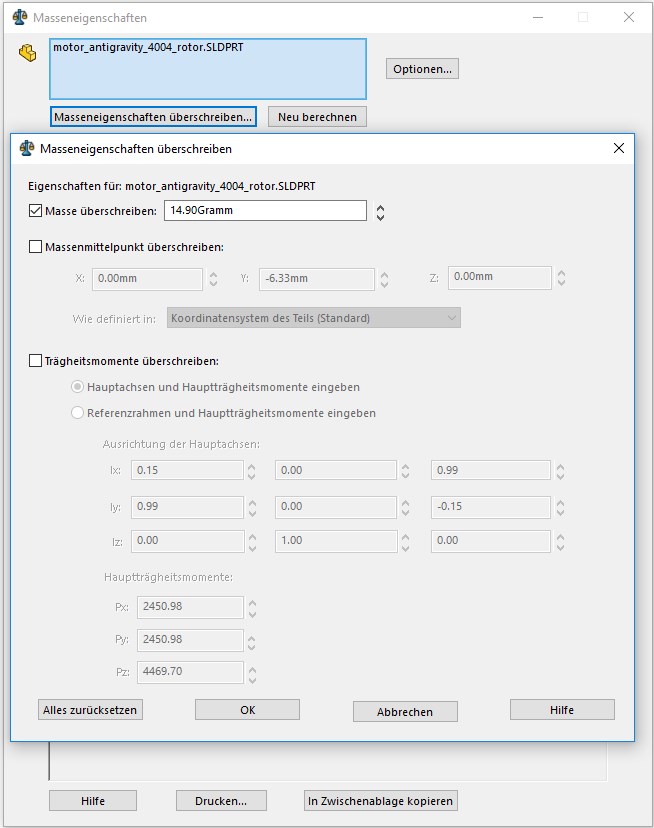
For parts made from different material or unknown density you can override the mass calculation and set the total weight manually. Determine the weight of all the parts with a weight scale. In Solidworks choose → Evaluate → Mass Properties → Override Mass Properties and input the correct mass. Example: The motor rotor consists of an aluminum frame with steel magnets. Therefore the weight has to be measured and set correctly in Solidworks.
Once the weight of all of the subcomponents is set open the assembly and verify that the combined weight is correct. In the case of the upper leg the total weight is 149g.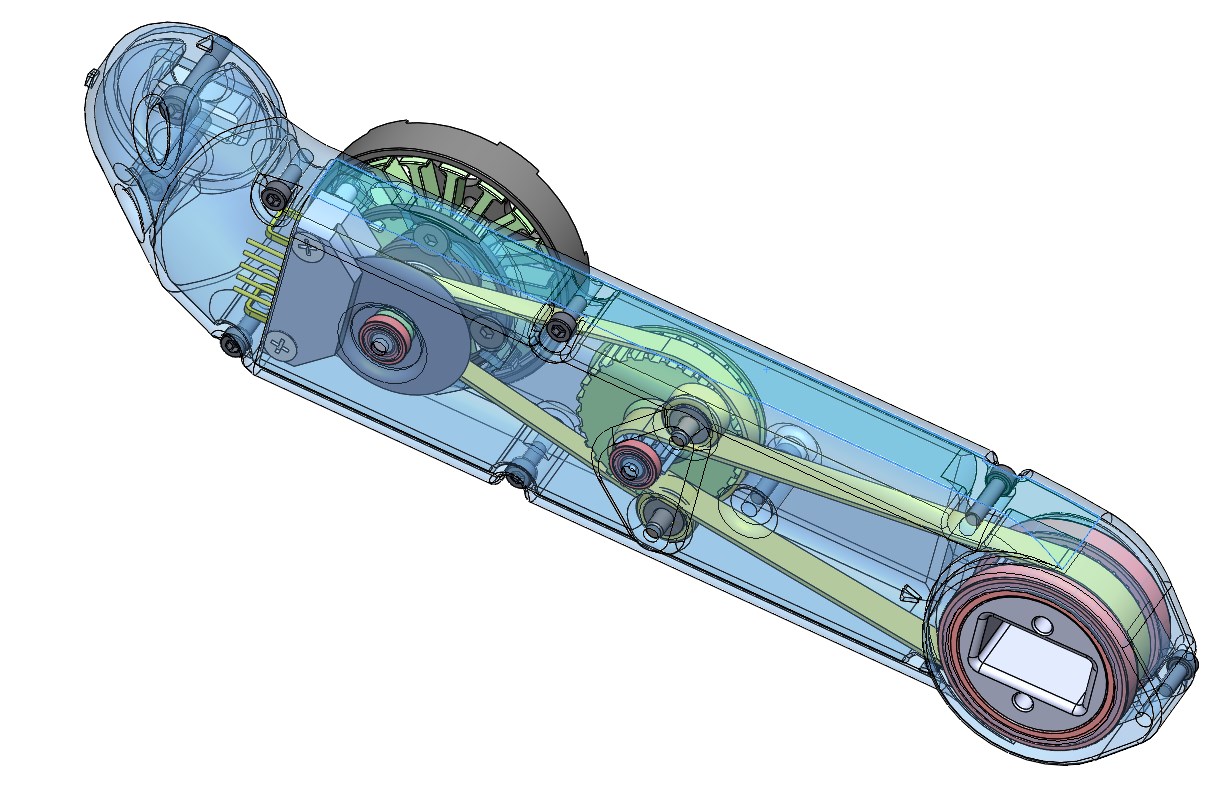
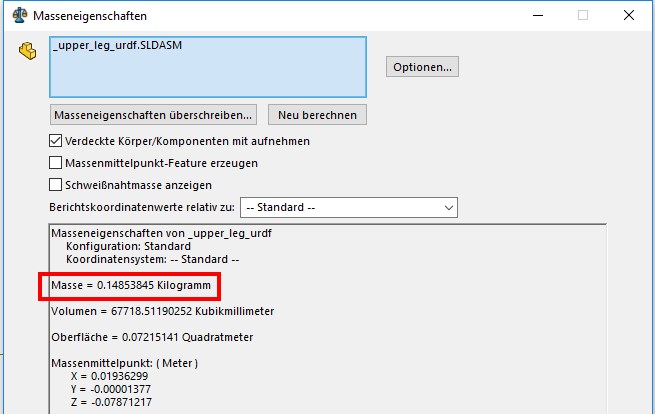
Create a coordinate system according to your conventions. The coordinate systems has to match the one from the STL files. Quadruped STL files for Visualisation Choose Evaluate → Mass Properties and set the output coordinate system to the one you created! For the quadruped robot we need a right and left version of the coordinate system.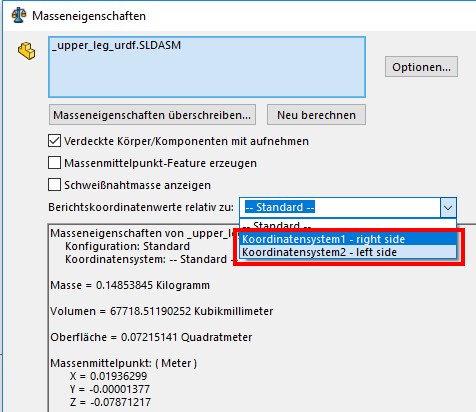
Set the units to Meters and Kilogramms. Set the precision to 8 decimal spaces.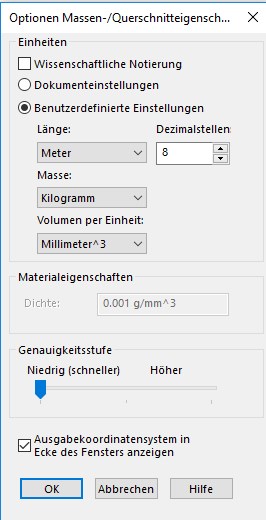
Copy and record the weight, the center of mass position and the inertia matrix. Use the second inertia matrix that Solidworks calculates. (Lxx / Lxy / Lxz / ...) That is the inertia of all the parts with respect to the center of mass and aligned to the coordinate system that you have defined. The URDF data required for the upper leg would be the following: Mass: 0.14853845 Kilogramm Center of Mass Position [m]: X = -0.00001377 Y = -0.01936299 Z = -0.07871217 Inertia Matrix: Trägheitsmomente: ( Kilogramm * Quadratmeter ) Bezogen auf den Massenmittelpunkt und ausgerichtet auf das Ausgabekoordinatensystem. Lxx = 0.00041100 Lxy = 0.00000000 Lxz = -0.00000009 Lyx = 0.00000000 Lyy = 0.00041184 Lyz = 0.00004668 Lzx = -0.00000009 Lzy = 0.00004668 Lzz = 0.00003022 Document all of the data on the Wiki.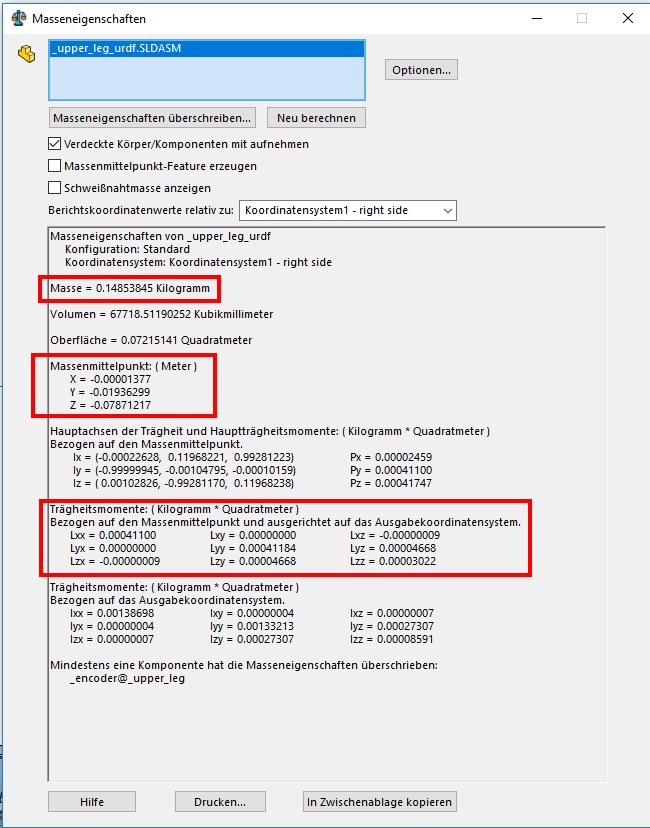